Free NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions solved by Expert Teachers as per NCERT (CBSE) Book guidelines and brought to you by CBSE Learning. These Inverse Trigonometric Functions Exercise Questions with Solutions for Class 12 Maths covers all questions of Chapter Inverse Trigonometric Functions Class 12 and help you to revise complete Syllabus and Score More marks as per CBSE Board guidelines from the latest NCERT book for class 12 maths. You can read and download NCERT Book Solution to get a better understanding of all topics and concepts
2.1 Introduction
2.2 Basic Concepts
2.3 Properties of Inverse Trigonometric Functions.
Inverse Trigonometric Functions NCERT Solutions – Class 12 Maths
Q1 : Find the principal value of ![]()
Answer :
Let ![]() =y. Then sin y=
=y. Then sin y=![]()
We know that the range of the principal value branch of sin-1 is
![]() and sin
and sin![]()
Therefore, the principal value of![]()
Q2 : Find the principal value of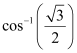
Answer :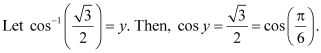
We know that the range of the principal value branch of cos -1is
![]()
Therefore, the principal value of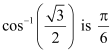 .
.
Q3 : Find the principal value of cosec-1(2)
Answer :
Let cosec -1(2) = y. Then,![]()
We know that the range of the principal value branch of cosec-1is ![]()
Therefore, the principal value of![]()
Q4 : Find the principal value of![]()
Answer :![]()
We know that the range of the principal value branch of tan -1is
![]()
Therefore, the principal value of![]()
Q5 : Find the principal value of![]()
Answer :![]()
We know that the range of the principal value branch of cos -1is
![]()
Therefore, the principal value of![]()
Q6 : Find the principal value of tan-1(-1)
Answer :
Let tan-1(-1) = y. Then,![]()
We know that the range of the principal value branch of tan-1 is![]()
Therefore, the principal value of![]()
Q7 : Find the principal value of![]()
Answer :![]()
We know that the range of the principal value branch of sec-1 is
![]()
Therefore, the principal value of![]()
Q8 :Find the principal value of![]()
Answer :![]()
We know that the range of the principal value branch of cot-1 is
(0,π) and ![]()
Therefore, the principal value of![]()
Q9 : Find the principal value of![]()
Answer :![]()
We know that the range of the principal value branch of cos-1 is [0,π] and
![]()
Therefore, the principal value of![]()
Q10 : Find the principal value of![]()
Answer :![]()
We know that the range of the principal value branch of cosec-1 is![]()
Therefore, the principal value of![]()
Q11 :Find the value of![]()
Answer :
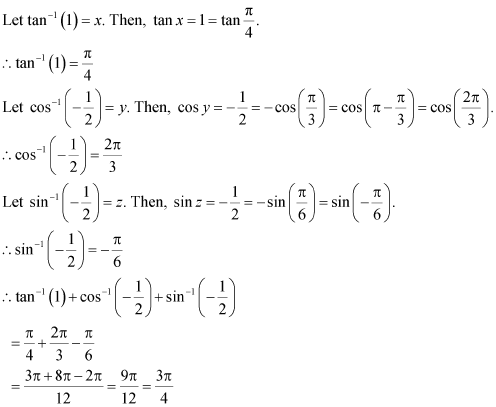
Q12 :Find the value of![]() Answer :
Answer :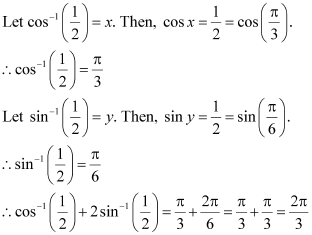
Q13 :Find the value of if sin – 1 x = y, then
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
Answer :
It is given that sin-1 x = y.
We know that the range of the principal value branch of sin-1 is![]()
Therefore,![]() .
.
Q14 :Find the value of![]() is equal to
is equal to
(A) π (B) ![]() (C)
(C)![]() (D)
(D)![]()
Answer
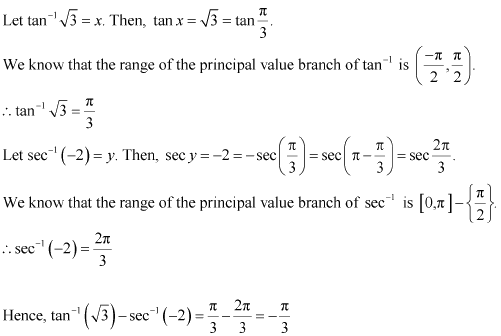
Exercise 2.2 : Solutions of Questions on Page Number : 47
Q1 :Prove ![]()
Answer :
To prove:![]()
Let x = sinθ. Then, ![]()
We have,
R.H.S. =![]()
![]()
= 3θ
![]()
= L.H.S.
Q2 :Prove![]()
Answer :
To prove:![]()
Let x = cosθ. Then, cos-1 x =θ.
We have,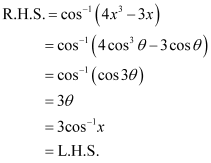
Q3 :Prove ![]()
Answer :
To prove:![]()
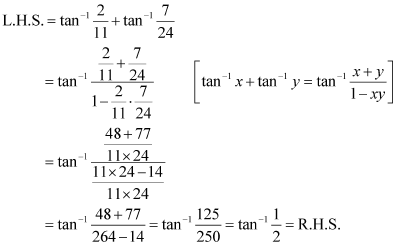
Q4 :Prove ![]()
Answer :
To prove:![]()
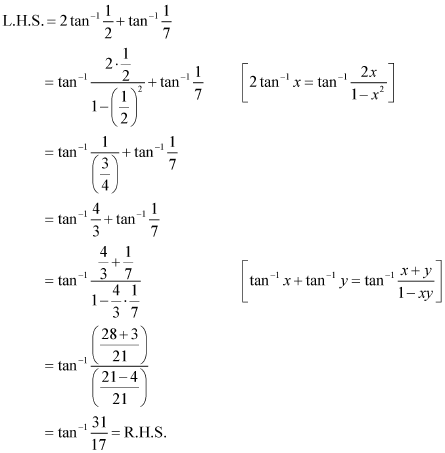
Q6 :Write the function in the simplest form:
![]()
Answer :![]()
Put x = cosec θ ⇒ θ = cosec-1 x
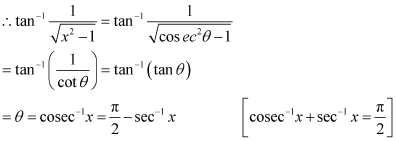
Q7 :Write the function in the simplest form: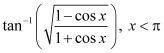
Answer :
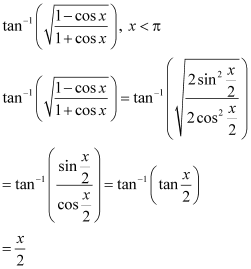
Q8 :Write the function in the simplest form:
![]()
Answer :
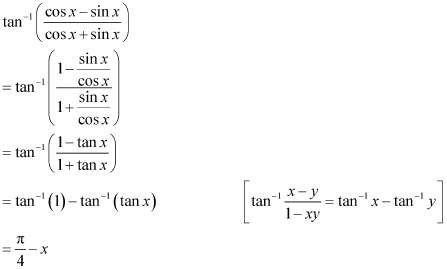
Q9 :Write the function in the simplest form:
![]()
Answer :
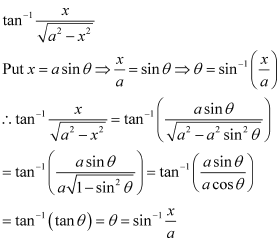
Q10 :Write the function in the simplest form:
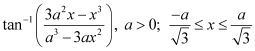
Answer :
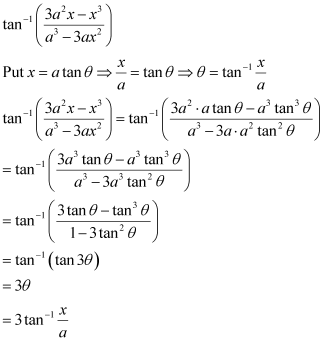
Q11 :Find the value of![]()
Answer :
Let![]() . Then,
. Then,![]()
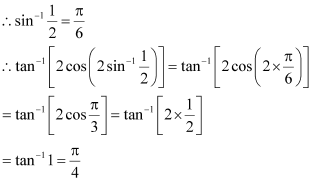
Q12 :Find the value of ![]()
Answer :
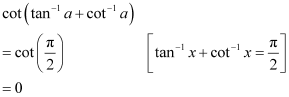
Q13 :Find the value of
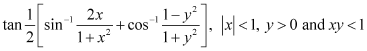
Answer :
Let x = tan θ. Then, θ = tan-1 x.
![]()
Let y = tan Φ. Then, Φ = tan-1 y.
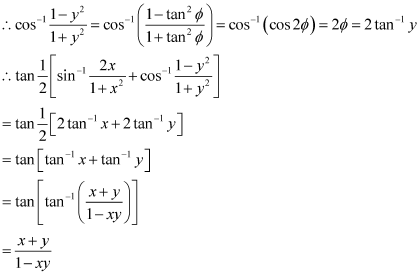
Q14 :If,![]() then find the value of x.
then find the value of x.
Answer :
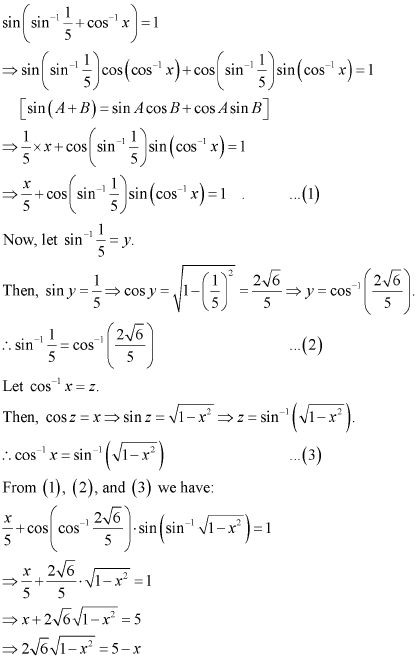
On squaring both sides, we get:
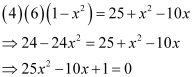
Hence, the value of x is![]()
Q15 :If, ![]() then find the value of x.
then find the value of x.
Answer :
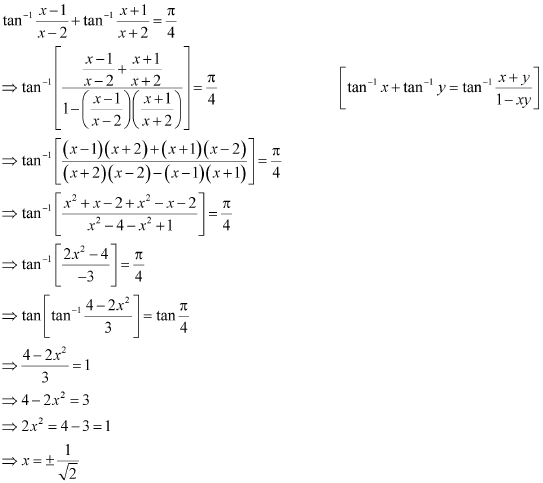
Hence, the value of x is![]()
Q16 :Find the values of ![]()
Answer :
![]()
We know that sin-1 (sin x) = x if![]() , which is the principal value branch of sin-1 x.
, which is the principal value branch of sin-1 x.
Here,![]()
Now,![]() can be written as:
can be written as:![]()
![]()
Q17 :Find the values of![]()
Answer :![]()
We know that tan-1 (tan x) = x if,![]() which is the principal value branch of tan-1x.
which is the principal value branch of tan-1x.
Here,![]()
Now,![]() can be written as:
can be written as:
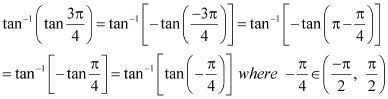
![]()
Q18 :Find the values of![]()
Answer :
Let. ![]() Then,
Then,![]()
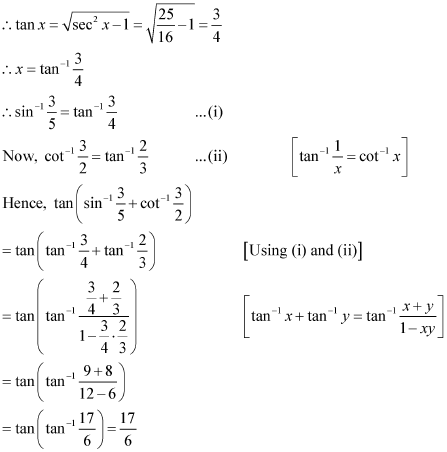
Q19 :Find the values of![]() is equal to
is equal to
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
Answer :
We know that cos-1 (cos x) = x if![]() , which is the principal value branch of cos-1 x.
, which is the principal value branch of cos-1 x.
Here,![]()
Now,![]() can be written as:
can be written as: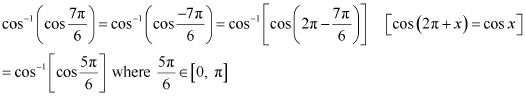
![]()
The correct answer is B.
Q20 :Find the values of ![]() is equal to
is equal to
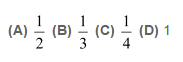
Answer :
Let ![]() . Then
. Then ![]()
We know that the range of the principle value branch of ![]()
![]()
![]()
The correct answer is D.
Q21 :Find the values of![]() is equal to
is equal to
(A) π (B) ![]() (C) 0 (D)
(C) 0 (D)![]()
Answer :
Let. ![]() Then,
Then,![]()
We know that the range of the principal value branch of![]()
![]() Let.
Let.![]()
![]()
The range of the principal value branch of![]()
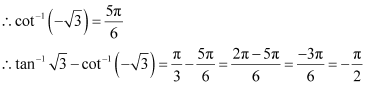 The correct answer is B.
The correct answer is B.
Exercise Miscellaneous : Solutions of Questions on Page Number : 51
Q1 :Find the value of![]()
Answer :
We know that cos-1 (cos x) = x if![]() , which is the principal value branch of cos-1 x.
, which is the principal value branch of cos-1 x.
Here,![]()
Now, ![]() can be written as:
can be written as: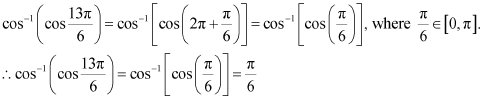
Q2 :Find the value of![]()
Answer :
We know that tan-1 (tan x) = x if![]() , which is the principal value branch of tan-1 x.
, which is the principal value branch of tan-1 x.
Here,![]()
Now,![]() can be written as:
can be written as: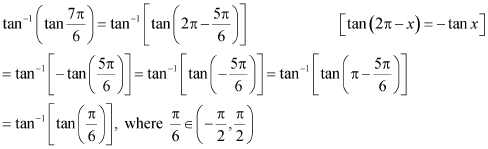
![]()
Q3 :Prove![]()
Answer :
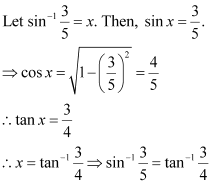
Now, we have:
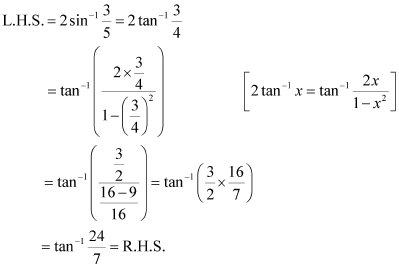
Q4 :Prove![]()
Answer :
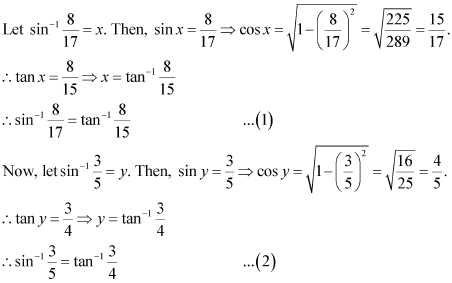
Now, we have:
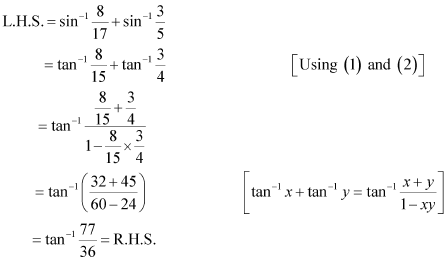
Q5 :Prove![]()
Answer :
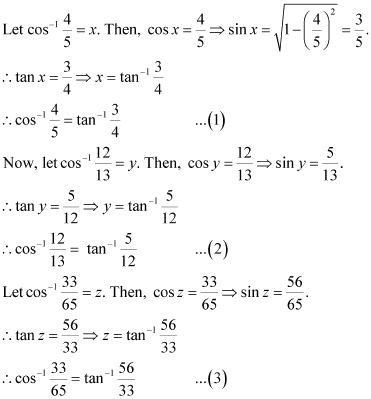
Now, we will prove that:
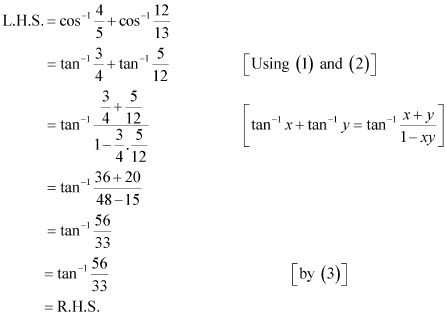
Q6 :Prove![]()
Answer :
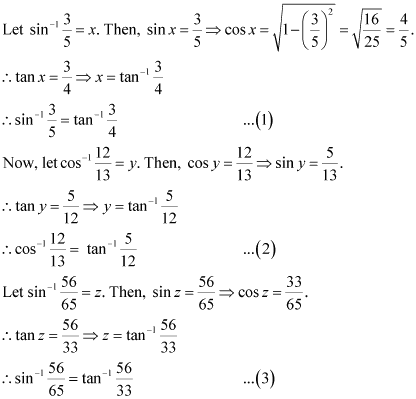
Now, we have:

Q7 :Prove![]()
Answer :
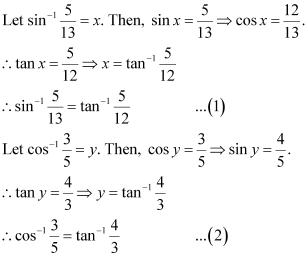
Using (1) and (2), we have
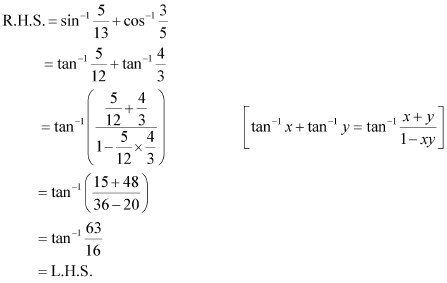
Q8 :Prove![]()
Answer :
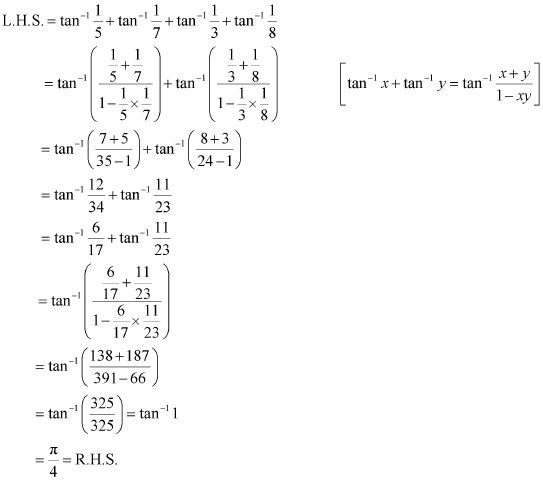
Q9 :Prove![]()
Answer :
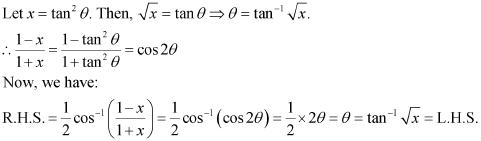
Q10 :Prove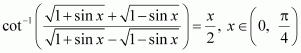
Answer :
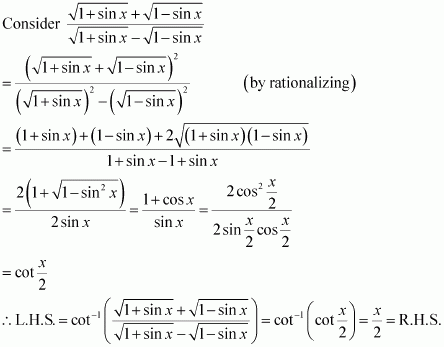
Q11 :Prove 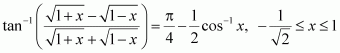 [Hint: putx = cos 2θ]
[Hint: putx = cos 2θ]
Answer :
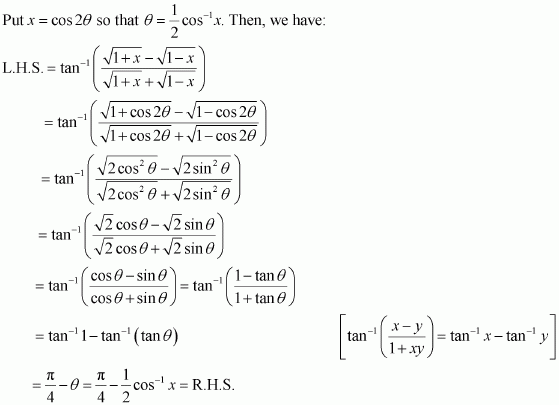
Q12 :Prove![]()
Answer :
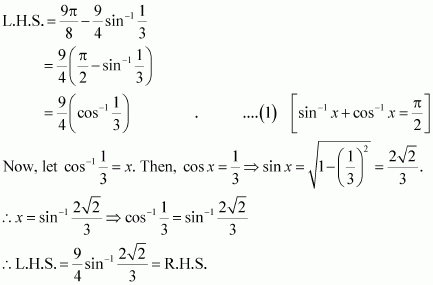
Q13 :Solve![]()
Answer :
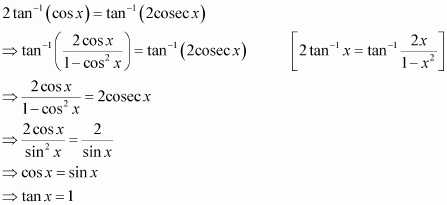
![]()
Q14: Solve ![]()
Answer:
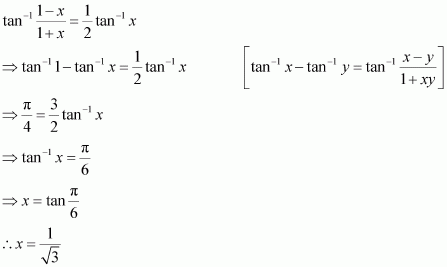
Q15 :Solve![]() is equal to
is equal to
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
Answer :
Let tan – 1 x = y. Then,![]()
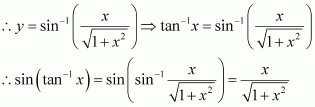
The correct answer is D.
Q16 :Solve,![]() then x is equal to
then x is equal to
(A) ![]() (B)
(B) ![]() (C) 0 (D)
(C) 0 (D)![]()
Answer :
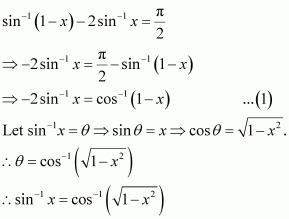
Therefore, from equation (1), we have
![]()
Put x = sin y. Then, we have:
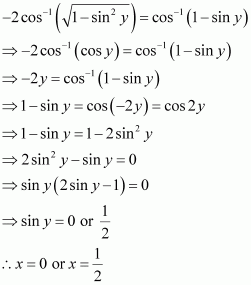
But, when![]() , it can be observed that:
, it can be observed that:
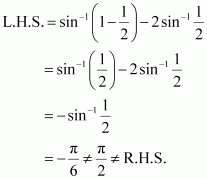
![]() is not the solution of the given equation.
is not the solution of the given equation.
Thus, x = 0.
Hence, the correct answer is C.
Q17 :Solve![]() is equal to
is equal to
(A) ![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
Answer :
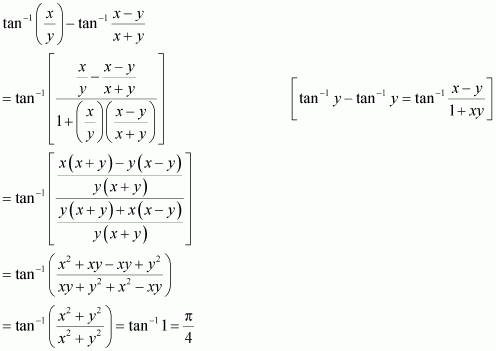
Hence, the correct answer is C.