NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry

Some Applications of Trigonometry NCERT Solutions – Class 10 Maths

Exercise 9.1 : Solutions of Questions on Page Number : 203

Q1 : A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30 °.

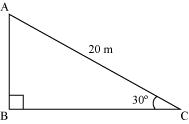
Answer :
It can be observed from the figure that AB is the pole.
In ΔABC,

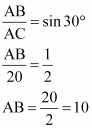
Therefore, the height of the pole is 10 m.

Q2 : A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30 ° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer :

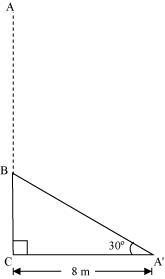
Let AC was the original tree. Due to storm, it was broken into two parts. The broken part is making 30° with the ground.
In ,

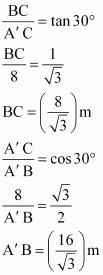
Height of tree = + BC

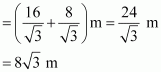
Hence, the height of the tree is.

Q3 : A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30 ° to the ground, where as for the elder children she wants to have a steep side at a height of 3 m, and inclined at an angle of 60 ° to the ground. What should be the length of the slide in each case?
Answer :
It can be observed that AC and PR are the slides for younger and elder children respectively.

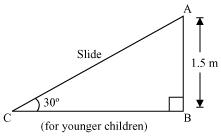
In ΔABC,

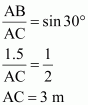
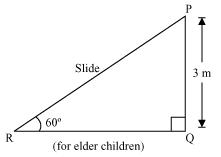
In ΔPQR,

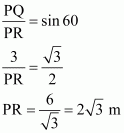
Therefore, the lengths of these slides are 3 m and .

Q4 : The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.
Answer :

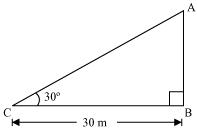
Let AB be the tower and the angle of elevation from point C (on ground) is
30°.
In ΔABC,

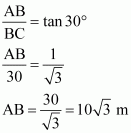
Therefore, the height of the tower is.

Q5 : A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Answer :

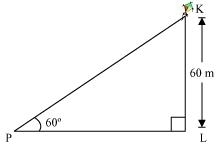
Let K be the kite and the string is tied to point P on the ground.
In ΔKLP,

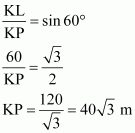
Hence, the length of the string is.

Q6 : A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Answer :

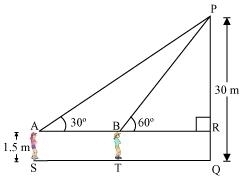
Let the boy was standing at point S initially. He walked towards the building and reached at point T.
It can be observed that
PR = PQ – RQ
= (30 – 1.5) m = 28.5 m =
In ΔPAR,

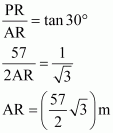
In ΔPRB,

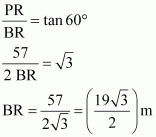
ST = AB

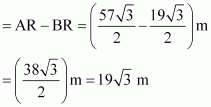
Hence, he walked towards the building.

Q7 : From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Answer :

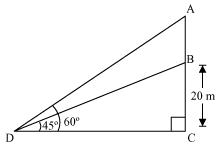
Let BC be the building, AB be the transmission tower, and D be the point on the ground from where the elevation angles are to be measured.
In ΔBCD,

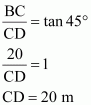
In ΔACD,

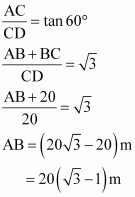
Therefore, the height of the transmission tower is m.

Q8 : A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45 °. Find the height of the pedestal.
Answer :

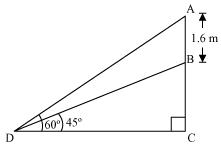
Let AB be the statue, BC be the pedestal, and D be the point on the ground from where the elevation angles are to be measured.
In ΔBCD,

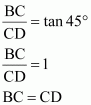
In ΔACD,

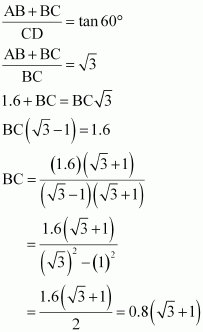
Therefore, the height of the pedestal is 0.8m.

Q9 : The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Answer :

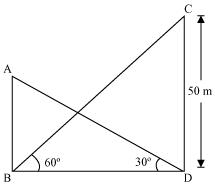
Let AB be the building and CD be the tower.
In ΔCDB,

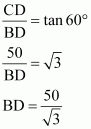
In ΔABD,

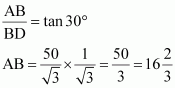
Therefore, the height of the building is.

Q10 : Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
Answer :

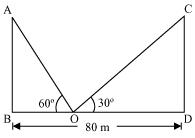
Let AB and CD be the poles and O is the point from where the elevation angles are measured.
In ΔABO,

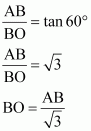
In ΔCDO,

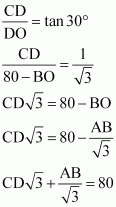
Since the poles are of equal heights,
CD = AB

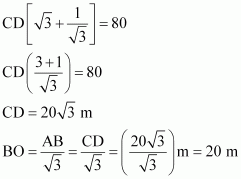
DO = BD – BO = (80 – 20) m = 60 m
Therefore, the height of poles isand the point is 20 m and 60 m far from these poles.

Q11 : A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

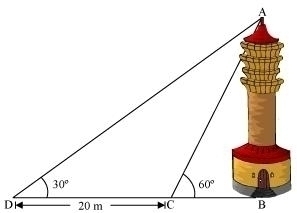
Answer :
In ΔABC,

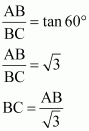
In ΔABD,

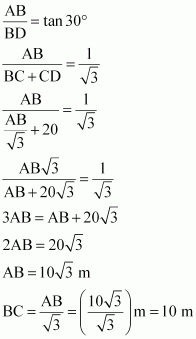
Therefore, the height of the tower is m and the width of the canal is
10 m.

Q12 : From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Answer :

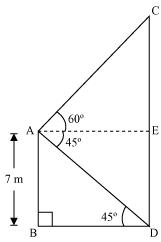
Let AB be a building and CD be a cable tower.
In ΔABD,

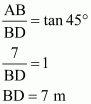
In ΔACE,
AE = BD = 7 m

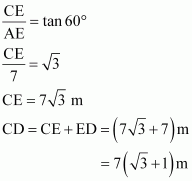
Therefore, the height of the cable tower is.

Q13 : As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Answer :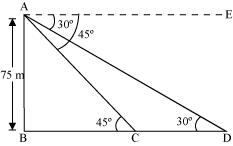

Let AB be the lighthouse and the two ships be at point C and D respectively.
In ΔABC,

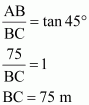
In ΔABD,

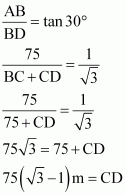
Therefore, the distance between the two ships ism.

Q14 : A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

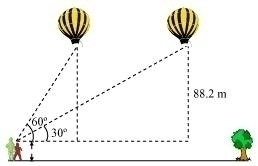
Answer :

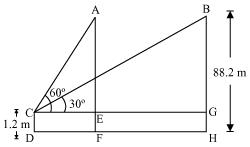
Let the initial position A of balloon change to B after some time and CD be the girl.
In ΔACE,

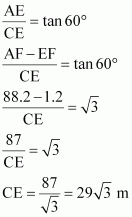
In ΔBCG,

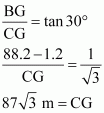
Distance travelled by balloon = EG = CG – CE

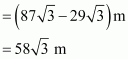
Q15 : A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Answer :

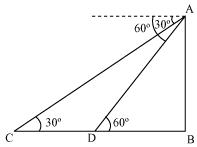
Let AB be the tower.
Initial position of the car is C, which changes to D after six seconds.
In ΔADB,

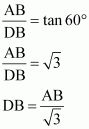
In ΔABC,

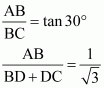
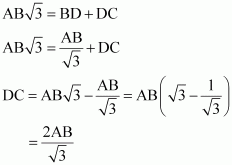
Time taken by the car to travel distance DC= 6 seconds
Time taken by the car to travel distance DB

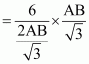
Q16 : The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Answer :

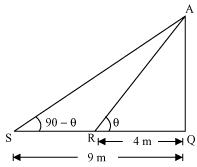
Let AQ be the tower and R, S are the points 4m, 9m away from the base of the tower respectively.
The angles are complementary. Therefore, if one angle is θ, the other will be 90 – θ.
In ΔAQR,

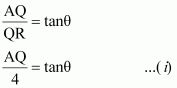
In ΔAQS,

On multiplying equations (i) and (ii), we obtain

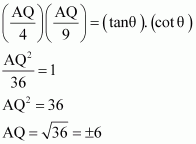
However, height cannot be negative.
Therefore, the height of the tower is 6 m.

NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry

Some Applications of Trigonometry NCERT Solutions – Class 10 Maths

NCERT Solutions for Class 10 Maths All Chapters