NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Introduction to Trigonometry Solutions – Class 10 Maths

Exercise 8.1 : Solutions of Questions on Page Number : 181

Q1 : In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine
(i) sin A, cos A
(ii) sin C, cos C
Answer :
Applying Pythagoras theorem for ΔABC, we obtain
AC² = AB² + BC²
= (24 cm)² + (7 cm)²
= (576 + 49) cm²
= 625 cm²
∴ AC = cm = 25 cm

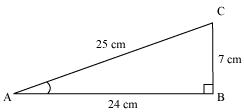
(i) sin A =

cos A =
(ii)

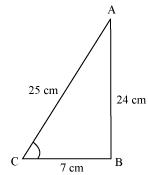
sin C =

cos C =

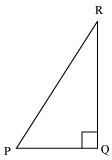
Q2 : In the given figure find tan P – cot R

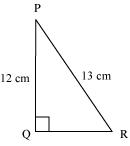
Answer :
Applying Pythagoras theorem for ΔPQR, we obtain
PR² = PQ² + QR²
(13 cm)² = (12 cm)² + QR²
169 cm² = 144 cm² + QR²
25 cm² = QR²
QR = 5 cm

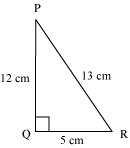
tan P – cot R =

Q3 : If sin A =, calculate cos A and tan A.
Answer :
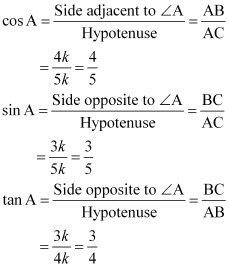
Let ΔABC be a right-angled triangle, right-angled at point B.

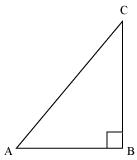
Given that,

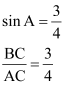
Let BC be 3k. Therefore, AC will be 4k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC² = AB² + BC²
(4k)² = AB² + (3k)²
16k² – 9k² = AB²
7k² = AB²
AB =

Q4 : Given 15 cot A = 8. Find sin A and sec A
Answer :
Consider a right-angled triangle, right-angled at B.

It is given that,
cot A =

Let AB be 8k.Therefore, BC will be 15k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC² = AB² + BC²
= (8k)² + (15k)²
= 64k² + 225k²
= 289k²
AC = 17k

Q5 : Given sec θ =, calculate all other trigonometric ratios.
Answer :
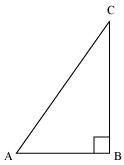
Consider a right-angle triangle ΔABC, right-angled at point B.

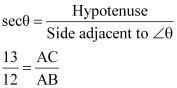
If AC is 13k, AB will be 12k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
(AC)² = (AB)² + (BC)²
(13k)² = (12k)² + (BC)²
169k² = 144k² + BC²
25k² = BC²
BC = 5k

Q6 : If ∠ A and ∠ B are acute angles such that cos A = cos B, then show that
∠ A = ∠ B.
Answer :
Let us consider a triangle ABC in which CD ⊥ AB.

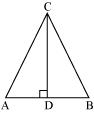
It is given that
cos A = cos B
… (1)
We have to prove ∠A = ∠B. To prove this, let us extend AC to P such that BC = CP.

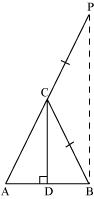
From equation (1), we obtain

By using the converse of B.P.T,
CD||BP
⇒∠ACD = ∠CPB (Corresponding angles) … (3)
And, ∠BCD = ∠CBP (Alternate interior angles) … (4)
By construction, we have BC = CP.
∴ ∠CBP = ∠CPB (Angle opposite to equal sides of a triangle) … (5)
From equations (3), (4), and (5), we obtain
∠ACD = ∠BCD … (6)
In ΔCAD and ΔCBD,
∠ACD = ∠BCD [Using equation (6)]
∠CDA = ∠CDB [Both 90°]
Therefore, the remaining angles should be equal.
∴∠CAD = ∠CBD
⇒ ∠A = ∠B
Alternatively,
Let us consider a triangle ABC in which CD ⊥ AB.

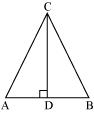
It is given that,
cos A = cos B

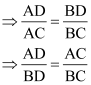
Let
⇒ AD = k BD … (1)
And, AC = k BC … (2)
Using Pythagoras theorem for triangles CAD and CBD, we obtain
CD² = AC² – AD² … (3)
And, CD² = BC² – BD² … (4)
From equations (3) and (4), we obtain
AC² – AD² = BC² – BD²
⇒ (k BC)² – (k BD)² = BC² – BD²
⇒ k² (BC² – BD²) = BC² – BD²
⇒ k² = 1
⇒ k = 1
Putting this value in equation (2), we obtain
AC = BC
⇒ ∠A = ∠B(Angles opposite to equal sides of a triangle)

Q7 : If cot θ =, evaluate
(i) (ii) cot2 θ
Answer :
Let us consider a right triangle ABC, right-angled at point B.

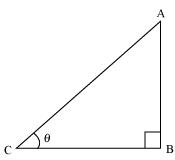
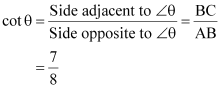
If BC is 7k, then AB will be 8k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC² = AB² + BC²
= (8k)² + (7k)²
= 64k² + 49k²
= 113k²
AC =

(i)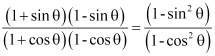

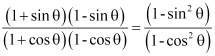
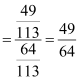
(ii) cot² θ = (cot θ)² = =

Q8 : If 3 cot A = 4, Check whether
Answer :
It is given that 3cot A = 4
Or, cot A =
Consider a right triangle ABC, right-angled at point B.

If AB is 4k, then BC will be 3k, where k is a positive integer.
In ΔABC,
(AC)² = (AB)² + (BC)²
= (4k)² + (3k)²
= 16k² + 9k²
= 25k²
AC = 5k

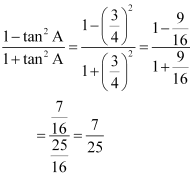
cos² A – sin² A =

∴

Q9 : In ΔABC, right angled at B. If, find the value of
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Answer :

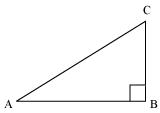
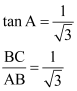
If BC is k, then AB will be, where k is a positive integer.
In ΔABC,
AC² = AB² + BC²
=
= 3k² + k² = 4k²
∴ AC = 2k

(i) sin A cos C + cos A sin C

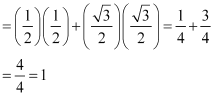
(ii) cos A cos C – sin A sin C

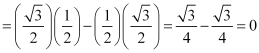
Q10 : In ΔPQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Answer :
Given that, PR + QR = 25
PQ = 5
Let PR be x.
Therefore, QR = 25 – x

Applying Pythagoras theorem in ΔPQR, we obtain
PR² = PQ² + QR²
x² = (5)² + (25 – x)²
x² = 25 + 625 + x² – 50x
50x = 650
x = 13
Therefore, PR = 13 cm
QR = (25 – 13) cm = 12 cm

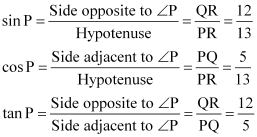
Q11 : State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A =for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A
(v) sin θ =, for some angle θ
Answer :
(i) Consider a ΔABC, right-angled at B.

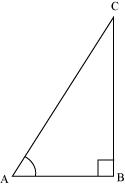
But > 1
∴tan A > 1
So, tan A < 1 is not always true.
Hence, the given statement is false.
(ii)

Let AC be 12k, AB will be 5k, where k is a positive integer.
Applying Pythagoras theorem in ΔABC, we obtain
AC² = AB² + BC²
(12k)² = (5k)² + BC²
144k² = 25k² + BC²
BC² = 119k²
BC = 10.9k
It can be observed that for given two sides AC = 12k and AB = 5k,
BC should be such that,
AC – AB < BC < AC + AB
12k – 5k < BC < 12k + 5k
7k < BC < 17 k
However, BC = 10.9k. Clearly, such a triangle is possible and hence, such value of sec A is possible.
Hence, the given statement is true.
(iii) Abbreviation used for cosecant of angle A is cosec A. And cos A is the abbreviation used for cosine of angle A.
Hence, the given statement is false.
(iv) cot A is not the product of cot and A. It is the cotangent of ∠A.
Hence, the given statement is false.
(v) sin θ =We know that in a right-angled triangle,
In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible.
Hence, the given statement is false

Exercise 8.2 : Solutions of Questions on Page Number : 187

Q1 : Evaluate the following
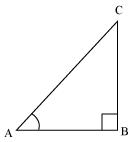
(i) sin60° cos30° + sin30° cos60°
(ii) 2tan²45° + cos²30° – sin²60°
(iii)
(iv)
(v)
Answer :
(i) sin60° cos30° + sin30° cos60°

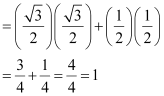
(ii) 2tan²45° + cos²30° – sin²60°

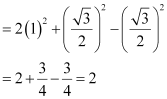
(iii)

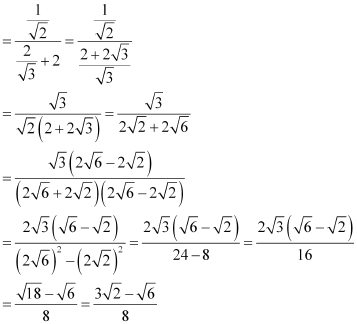
(iv)

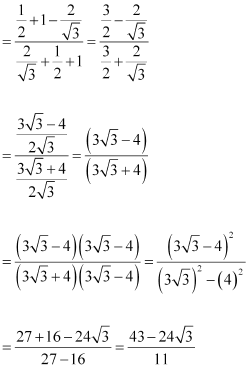
(v)

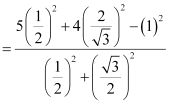
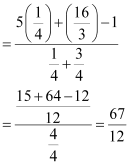
Q2 : Choose the correct option and justify your choice.
(i)

(A). sin60°
(B). cos60°
(C). tan60°
(D). sin30°
(ii)
(A). tan90°
(B). 1
(C). sin45°
(D). 0
(iii) sin2A = 2sinA is true when A =
(A). 0°
(B). 30°
(C). 45°
(D). 60°
(iv)
(A). cos60°
(B). sin60°
(C). tan60°
(D). sin30°
Answer :
(i)

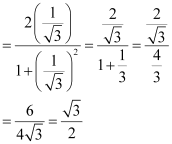
Out of the given alternatives, only
Hence, (A) is correct.
(ii)

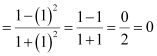
Hence, (D) is correct.
(iii)Out of the given alternatives, only A = 0° is correct.
As sin 2A = sin 0° = 0
2 sinA = 2sin 0° = 2(0) = 0
Hence, (A) is correct.
(iv)

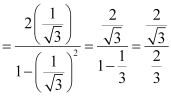
Out of the given alternatives, only tan 60°
Hence, (C) is correct.

Q3 : If and;
0° < A + B ≤90°, A > B find A and B.
Answer :

⇒
⇒ A + B = 60 … (1)

⇒ tan (A – B) = tan30
⇒ A – B = 30 … (2)
On adding both equations, we obtain
2A = 90
⇒ A = 45
From equation (1), we obtain
45 + B = 60
B = 15
Therefore, ∠A = 45° and ∠B = 15°

Q4 : State whether the following are true or false. Justify your answer.
(i) sin(A + B) = sin A + sin B
(ii) The value of sinθ¸increases as θ¸increases
(iii) The value of cos θ¸increases as θ¸increases
(iv) sinθ¸= cos θ¸ for all values of θ¸
(v) cot A is not defined for A = 0°
Answer :
(i) sin(A + B) = sin A + sin B
Let A = 30° and B = 60°
sin (A + B) = sin (30° + 60°)
= sin 90°
= 1

sin A + sin B = sin 30° + sin 60°
Clearly, sin (A + B) ≠sin A + sin B
Hence, the given statement is false.
(ii) The value of sin θ increases as θ increases in the interval of 0° < θ < 90° as
sin 0° = 0

sin 90° = 1
Hence, the given statement is true.
(iii) cos 0° = 1

cos90° = 0
It can be observed that the value of cos θ does not increase in the interval of 0° < θ < 90°.
Hence, the given statement is false.
(iv) sin θ = cos θ for all values of θ.
This is true when θ = 45°
As

It is not true for all other values of θ.
As and ,
Hence, the given statement is false.
(v) cot A is not defined for A = 0°
As ,
= undefined
Hence, the given statement is true.

Exercise 8.3 : Solutions of Questions on Page Number : 189

Q1 : Evaluate
(I)
(II)
(III) cos 48° – sin 42°
(IV) cosec 31° – sec 59°
Answer :
(I)

(II)

(III)cos 48° – sin 42° = cos (90° – 42°) – sin 42°
= sin 42° – sin 42°
= 0
(IV) cosec 31° – sec 59° = cosec (90° – 59°) – sec 59°
= sec 59° – sec 59°
= 0

Q2 : Show that
(I) tan 48° tan 23° tan 42° tan 67° = 1
(II)cos 38° cos 52° – sin 38° sin 52° = 0
Answer :
(I) tan 48° tan 23° tan 42° tan 67°
= tan (90° – 42°) tan (90° – 67°) tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°) (cot 67° tan 67°)
= (1) (1)
= 1
(II) cos 38° cos 52° – sin 38° sin 52°
= cos (90° – 52°) cos (90°-38°) – sin 38° sin 52°
= sin 52° sin 38° – sin 38° sin 52°
= 0

Q3 : If tan 2A = cot (A- 18°), where 2A is an acute angle, find the value of A.
Answer :
Given that,
tan 2A = cot (A- 18°)
cot (90° – 2A) = cot (A -18°)
90° – 2A = A- 18°
108° = 3A
A = 36°

Q4 : If tan A = cot B, prove that A + B = 90°
Answer :
Given that,
tan A = cot B
tan A = tan (90° – B)
A = 90° – B
A + B = 90°

Q5 : If sec 4A = cosec (A- 20°), where 4A is an acute angle, find the value of A.
Answer :
Given that,
sec 4A = cosec (A – 20°)
cosec (90° – 4A) = cosec (A – 20°)
90° – 4A= A- 20°
110° = 5A
A = 22°

Q6 : If A, Band C are interior angles of a triangle ABC then show that

Answer :
We know that for a triangle ABC,
∠ A + ∠B + ∠C = 180°
∠B + ∠C= 180° – ∠A

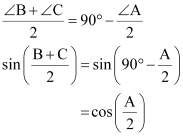
Q7 : Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Answer :
sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°

Exercise 8.4 : Solutions of Questions on Page Number : 193

Q1 : Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Answer :
We know that,

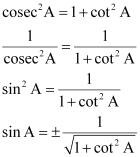
will always be positive as we are adding two positive quantities.
Therefore,
We know that,
However,
Therefore,
Also,

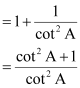
Q2 : Write all the other trigonometric ratios of ∠ A in terms of sec A.
Answer :
We know that,

Also, sin² A + cos² A = 1
sin² A = 1 – cos² A

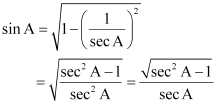
tan²A + 1 = sec²A
tan²A = sec²A – 1

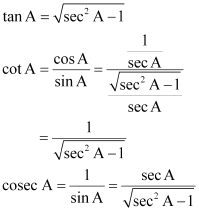
Q3 : Evaluate
(i)
(ii) sin25° cos65° + cos25° sin65°
Answer :
(i)

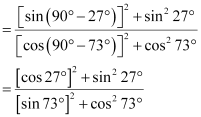
(As sin²A + cos²A = 1)
= 1
(ii) sin25° cos65° + cos25° sin65°

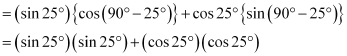
= sin²25° + cos²25°
= 1 (As sin²A + cos²A = 1)

Q4 : Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0
(B) 1
(C) 2
(D) – 1
(iii) (secA + tanA) (1 – sinA) =
(A) secA
(B) sinA
(C) cosecA
(D) cosA
(iv)
(A) sec² A
(B) – 1
(C) cot² A
(D) tan² A
Answer :
(i) 9 sec²A – 9 tan²A
= 9 (sec²A – tan²A)
= 9 (1) [As sec² A – tan² A = 1]
= 9
Hence, alternative (B) is correct.
(ii)
(1 + tan θ + sec θ) (1 + cot θ – cosec θ)

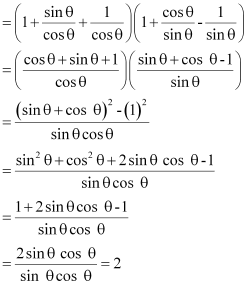
Hence, alternative (C) is correct.
(iii) (secA + tanA) (1 – sinA)
= cosA

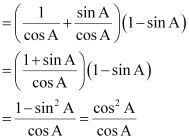
Hence, alternative (D) is correct.
(iv)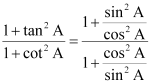

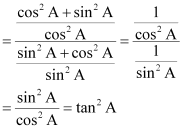
Hence, alternative (D) is correct.

Q5 : Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
Answer :
(i)

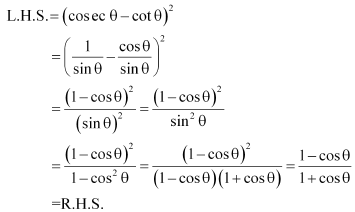
(ii)

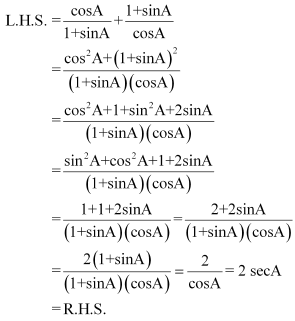
(iii)

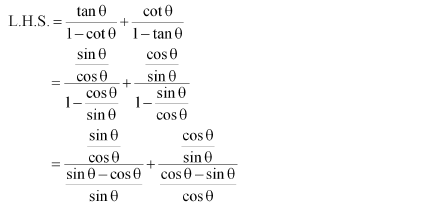
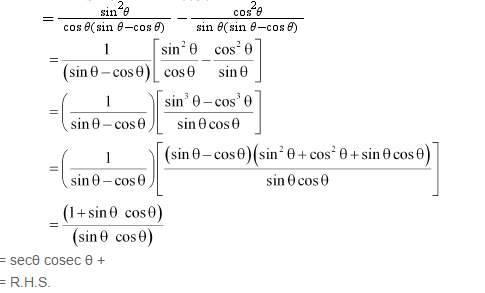
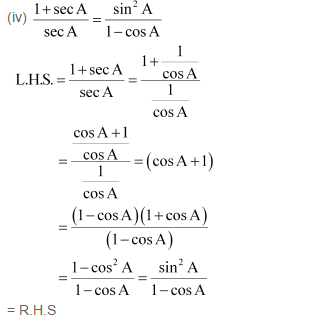
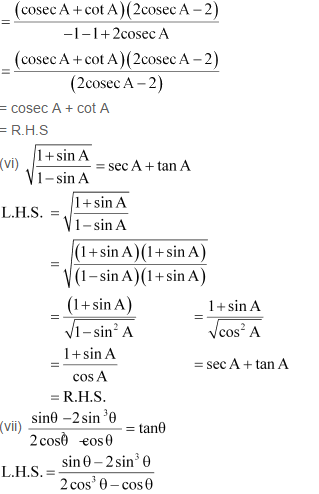
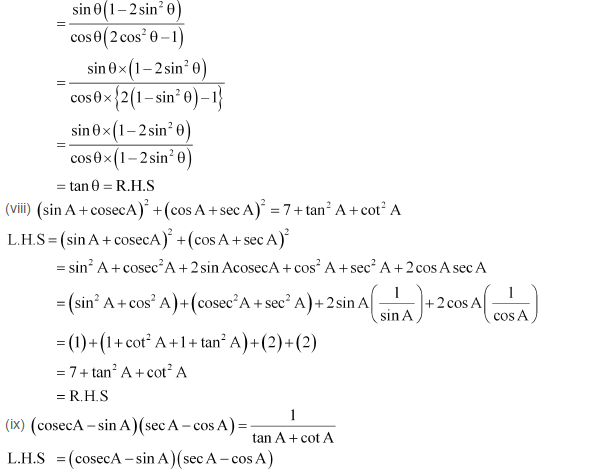
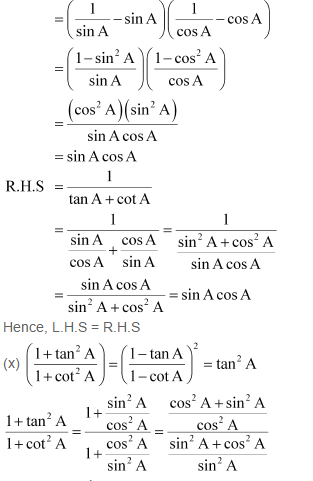
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Introduction to Trigonometry Solutions – Class 10 Maths

NCERT Solutions for Class 10 Maths All Chapters