Exercise : Solutions of Questions on Page Number : 152
Q1 :What will be the minimum pressure required to compress 500 dm3 of air at 1 bar to 200 dm3 at 30°C?
Answer :
Given,
Initial pressure, p1 = 1 bar
Initial volume, V1 = 500 dm3
Final volume, V2 = 200 dm3
Since the temperature remains constant, the final pressure (p2) can be calculated using Boyle’s law.
According to Boyle’s law,
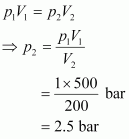
Therefore, the minimum pressure required is 2.5 bar.
Q2 :A vessel of 120 mL capacity contains a certain amount of gas at 35 °C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35 °C. What would be its pressure?
Answer :
Given,
Initial pressure, p1 = 1.2 bar
Initial volume, V1 = 120 mL
Final volume, V2 = 180 mL
Since the temperature remains constant, the final pressure (p2) can be calculated using Boyle’s law.
According to Boyle’s law,
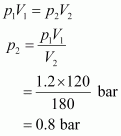
Therefore, the pressure would be 0.8 bar.
Q3 :Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressurep.
Answer :
The equation of state is given by,
pV = nRT ……….. (i)
Where,
p â- Pressure of gas
V â- Volume of gas
nâ- Number of moles of gas
R â- Gas constant
T â-Temperature of gas
From equation (i) we have,
![]()
Replacing n with ![]() , we have
, we have
![]()
Where,
m â-Mass of gas
M â-Molar mass of gas
But ![]() , (d = density of gas)
, (d = density of gas)
Thus, from equation (ii), we have
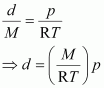
Molar mass (M) of a gas is always constant and therefore, at constant temperature ![]() = constant.
= constant.
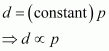
Hence, at a given temperature, the density (d) of gas is proportional to its pressure (p)
Q4 :At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?
Answer :
Density (d) of the substance at temperature (T) can be given by the expression,
d =![]()
Now, density of oxide (d1) is given by,
![]()
Where, M1 and p1 are the mass and pressure of the oxide respectively.
Density of dinitrogen gas (d2) is given by,
![]()
Where, M2 and p2 are the mass and pressure of the oxide respectively.
According to the given question,
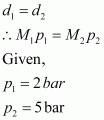
Molecular mass of nitrogen, M2 = 28 g/mol
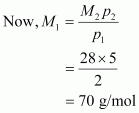
Hence, the molecular mass of the oxide is 70 g/mol.
Q5 :Pressure of 1 g of an ideal gas A at 27 °C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at same temperature the pressure becomes 3 bar. Find a relationship between their molecular masses.
Answer :
For ideal gas A, the ideal gas equation is given by,
pAV=nART………(i)
Where, pA and nA represent the pressure and number of moles of gas A.
pBV=nBRT………(ii)
For ideal gas B, the ideal gas equation is given by,
Where, pB and nB represent the pressure and number of moles of gas B.
[V and T are constants for gases A and B]
From equation (i), we have
![]()
From equation (ii), we have
![]()
Where, MA and MB are the molecular masses of gases A and B respectively.
Now, from equations (iii) and (iv), we have
![]()
Given,
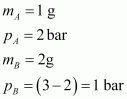
(Since total pressure is 3 bar)
Substituting these values in equation (v), we have
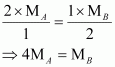
Thus, a relationship between the molecular masses of A and B is given by
![]()
Q6 :The drain cleaner, Drainex contains small bits of aluminum which react with caustic soda to produce dihydrogen. What volume of dihydrogen at 20 °C and one bar will be released when 0.15g of aluminum reacts?
Answer :
The reaction of aluminium with caustic soda can be represented as:
![]()
At STP (273.15 K and 1 atm), 54 g (2 × 27 g) of Al gives 3 × 22400 mL of H2..
0.15 g Al gives![]() i.e., 186.67 mL of H2.
i.e., 186.67 mL of H2.
At STP,
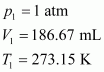
Let the volume of dihydrogen be at p2 = 0.987 atm (since 1 bar = 0.987 atm) and T2 = 20°C = (273.15 + 20) K = 293.15 K..
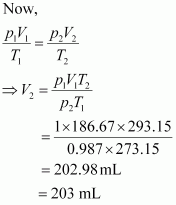
Therefore, 203 mL of dihydrogen will be released.
Q7 :What will be the pressure exerted by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm3 flask at 27 °C ?
Answer :
It is known that,
![]()
For methane (CH 4)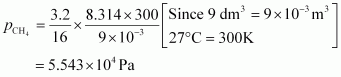
For carbon dioxide (CO2),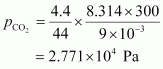
Total pressure exerted by the mixture can be obtained as:
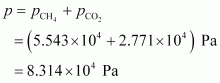
Hence, the total pressure exerted by the mixture is 8.314 × 104 Pa.
Q8 :What will be the pressure of the gaseous mixture when 0.5 L of H2 at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1L vessel at 27°C?
Answer :
Let the partial pressure of H2 in the vessel be.
Now,
p1=0.8 bar p2=pH2=?
V1=0.5L V2=1L
It is known that,
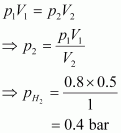
Now, let the partial pressure of O2 in the vessel be.
p1V1=p2
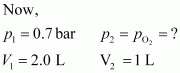
Q9 :Density of a gas is found to be 5.46 g/dm3 at 27 °C at 2 bar pressure. What will be its density at STP?
Answer :
Given,
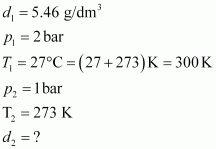
The density (d2) of the gas at STP can be calculated using the equation,
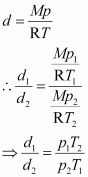
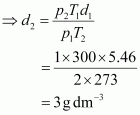
Hence, the density of the gas at STP will be 3 g dm-3
Q10 :34.05 mL of phosphorus vapour weighs 0.0625 g at 546 °C and 0.1 bar pressure. What is the molar mass of phosphorus?
Answer :
Given,
p = 0.1 bar
V = 34.05 mL = 34.05 × 10-3 L = 34.05 × 10-3 dm3
R = 0.083 bar dm3 K-1 mol-1
T = 546°C = (546 + 273) K = 819 K
The number of moles (n) can be calculated using the ideal gas equation as:
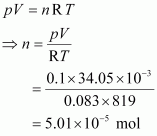
Therefore, molar mass of phosphorus ![]() = 1247.5 g mol-1
= 1247.5 g mol-1
Hence, the molar mass of phosphorus is 1247.5 g mol-1.
Q11 :A student forgot to add the reaction mixture to the round bottomed flask at 27 °C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake, and using a pyrometer he found the temperature of the flask was 477 °C. What fraction of air would have been expelled out?
Answer :
Let the volume of the round bottomed flask be V.
Then, the volume of air inside the flask at 27° C is V.
Now,
V1 = V
T1 = 27°C = 300 K
V2 =?
T2 = 477° C = 750 K
According to Charles’s law,
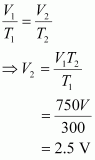
Therefore, volume of air expelled out = 2.5 V – V = 1.5 V
Hence, fraction of air expelled out ![]()
![]()
Q12 :Calculate the temperature of 4.0 mol of a gas occupying 5 dm3 at 3.32 bar.
(R = 0.083 bar dm3 K-1 mol-1).
Answer :
Given,
n = 4.0 mol
V = 5 dm3
p = 3.32 bar
R = 0.083 bar dm3 K-1 mol-1
The temperature (T) can be calculated using the ideal gas equation as:
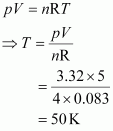
Hence, the required temperature is 50 K.
Q13 :Calculate the total number of electrons present in 1.4 g of dinitrogen gas.
Answer :
Molar mass of dinitrogen (N2) = 28 g mol-1
Thus, 1.4 g of ![]()
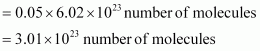
Now, 1 molecule of contains 14 electrons.
Therefore, 3.01 × 1023 molecules of N2 contains = 1.4 × 3.01 × 1023
= 4.214 × 1023 electrons
Q14 :How much time would it take to distribute one Avogadro number of wheat grains, if 1010 grains are distributed each second?
Answer :
Avogadro number = 6.02 × 1023
Thus, time required
=![]()
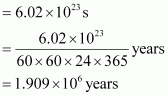
Hence, the time taken would be ![]() .
.
Q15 :Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm3 at 27°C. R = 0.083 bar dm3 K-1 mol-1.
Answer :
Given,
Mass of dioxygen (O2) = 8 g
Thus, number of moles of ![]()
Mass of dihydrogen (H2) = 4 g
Thus, number of moles of ![]()
Therefore, total number of moles in the mixture = 0.25 + 2 = 2.25 mole
Given,
V = 1 dm3
n = 2.25 mol
R = 0.083 bar dm3 K-1 mol-1
T = 27°C = 300 K
Total pressure (p) can be calculated as:
pV = nRT
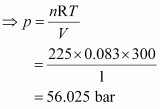
Hence, the total pressure of the mixture is 56.025 bar.
Q16 :Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10 m, mass 100 kg is filled with helium at 1.66 bar at 27°C. (Density of air = 1.2 kg m-3 and R = 0.083 bar dm3 K-1 mol-1).
Answer :
Given,
Radius of the balloon, r = 10 m
Volume of the balloon ![]()
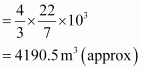
Thus, the volume of the displaced air is 4190.5 m3.
Given,
Density of air = 1.2 kg m-3
Then, mass of displaced air = 4190.5 × 1.2 kg
= 5028.6 kg
Now, mass of helium (m) inside the balloon is given by,

Now, total mass of the balloon filled with helium = (100 + 1117.5) kg
= 1217.5 kg
Hence, pay load = (5028.6-1217.5) kg
= 3811.1 kg
Hence, the pay load of the balloon is 3811.1 kg.
Q17 :Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure.
R = 0.083 bar L K-1 mol-1.
Answer :
It is known that,
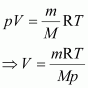
Here,
m = 8.8 g
R = 0.083 bar LK-1 mol-1
T = 31.1°C = 304.1 K
M = 44 g
p = 1 bar
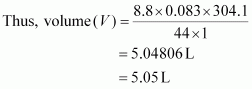
Hence, the volume occupied is 5.05 L.
Q18 :2.9 g of a gas at 95 °C occupied the same volume as 0.184 g of dihydrogen at 17 °C, at the same pressure. What is the molar mass of the gas?
Answer :
Volume (V) occupied by dihydrogen is given by,
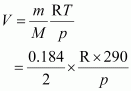
Let M be the molar mass of the unknown gas. Volume (V) occupied by the unknown gas can be calculated as:
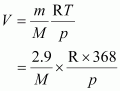
According to the question,
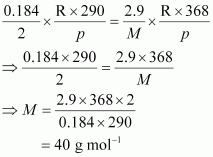
Hence, the molar mass of the gas is 40 g mol-1.
Q19 :A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.
Answer :
Let the weight of dihydrogen be 20 g and the weight of dioxygen be 80 g.
Then, the number of moles of dihydrogen,![]() and the number of moles of dioxygen,
and the number of moles of dioxygen,![]() .
.
Given,
Total pressure of the mixture, ptotal = 1 bar
Then, partial pressure of dihydrogen,
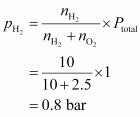
Hence, the partial pressure of dihydrogen is 0.8 bar.
Q20 :What would be the SI unit for the quantity pV2T 2/n?
Answer :
The SI unit for pressure, p is Nm-2.
The SI unit for volume, V is m3.
The SI unit for temperature, T is K.
The SI unit for the number of moles, n is mol.
Therefore, the SI unit for quantity ![]() is given by,
is given by,
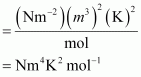
Q21 :In terms of Charles’ law explain why -273°C is the lowest possible temperature.
Answer :
Charles’ law states that at constant pressure, the volume of a fixed mass of gas is directly proportional to its absolute temperature.
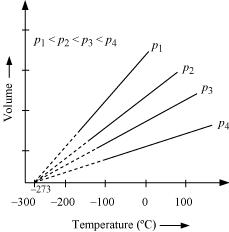
It was found that for all gases (at any given pressure), the plots of volume vs. temperature (in °C) is a straight line. If this line is extended to zero volume, then it intersects the temperature-axis at – 273°C. In other words, the volume of any gas at -273°C is zero. This is because all gases get liquefied before reaching a temperature of – 273°C. Hence, it can be concluded that – 273°C is the lowest possible temperature.
Q22 :Critical temperature for carbon dioxide and methane are 31.1 °C and -81.9 °C respectively. Which of these has stronger intermolecular forces and why?
Answer :
Higher is the critical temperature of a gas, easier is its liquefaction. This means that the intermolecular forces of attraction between the molecules of a gas are directly proportional to its critical temperature. Hence,
intermolecular forces of attraction are stronger in the case of CO2.
Q23 :Explain the physical significance of Van der Waals parameters.
Answer :
Physical significance of ‘a’:
‘a’ is a measure of the magnitude of intermolecular attractive forces within a gas.
Physical significance of ‘b’:
‘b’ is a measure of the volume of a gas molecule.