Exercise 9.1 : Solutions of Questions on Page Number : 140
Q1 : Identify the terms, their coefficients for each of the following expressions.
(i) 5xyz2 – 3zy
(ii) 1 + x + x2
(iii) 4x2y2 – 4x2y2z2 + z2
(iv) 3 – pq + qr – rp
(v)![]()
(vi) 0.3a – 0.6ab + 0.5b
Answer :
The terms and the respective coefficients of the given expressions are as follows.
| – | Terms | Coefficients |
| (i) | 5xyz2 – 3zy |
5 – 3 |
| (ii) | 1 x x2 |
1 1 1 |
| (iii) | 4x2y2 – 4x2y2z2 z2 |
4 – 4 1 |
| (iv) | 3 – pq qr – rp |
3 – 1 1 – 1 |
| (v) | – xy |
– 1 |
| (vi) | 0.3a – 0.6ab 0.5b |
0.3 – 0.6 0.5 |
Q2 : Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x2 + x3 + x4, 7 + y + 5x, 2y – 3y2, 2y – 3y2 + 4y3, 5x – 4y + 3xy, 4z – 15z2, ab + bc + cd + da, pqr, p2q + pq2, 2p + 2q
Answer :
The given expressions are classified as
Monomials: 1000, pqr
Binomials: x + y, 2y – 3y2, 4z – 15z2, p2q + pq2, 2p + 2q
Trinomials: 7 + y + 5x, 2y – 3y2 + 4y3, 5x – 4y + 3xy
Polynomials that do not fit in any of these categories are
x+ x2+ x3+ x4, ab + bc + cd + da
Q3 : Add the following.
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
(iv) l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + 2nl
Answer :
The given expressions written in separate rows, with like terms one below the other and then the addition of these expressions are as follows.
(i)
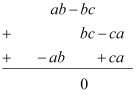
Thus, the sum of the given expressions is 0.
(ii)
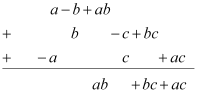
Thus, the sum of the given expressions is ab + bc + ac.
(iii)
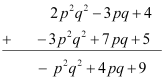
Thus, the sum of the given expressions is – p2q2 + 4pq + 9.
(iv)
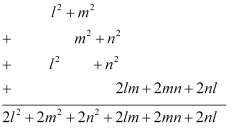
Thus, the sum of the given expressions is 2(l2 + m2 + n2 + lm + mn + nl).
Q4 : (a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
Answer :
The given expressions in separate rows, with like terms one below the other and then the subtraction of these expressions is as follows.
(a)
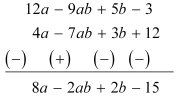
(b)
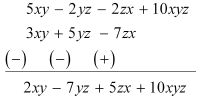
(c)
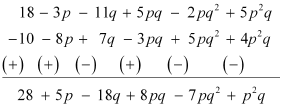
Exercise 9.2 : Solutions of Questions on Page Number : 143
Q1 : Find the product of the following pairs of monomials.
(i) 4, 7p (ii) – 4p, 7p (iii) – 4p, 7pq
(iv) 4p3, – 3p (v) 4p, 0
Answer :
The product will be as follows.
(i) 4 x 7p = 4 x 7 x p = 28p
(ii) – 4p x 7p = – 4 x p x 7 x p = (- 4 x 7) x (p x p) = – 28 p2
(iii) – 4p x 7pq = – 4 x p x 7 x p x q = (- 4 x 7) x (p x p x q) = – 28p2q
(iv) 4p3 x – 3p = 4 x (- 3) x p x p x p x p = – 12 p4
(v) 4p x 0 = 4 x p x 0 = 0
Q2 : Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x2, 5y2); (4x, 3x2); (3mn, 4np)
Answer :
We know that,
Area of rectangle = Length x Breadth
Area of 1st rectangle = p x q = pq
Area of 2nd rectangle = 10m x 5n = 10 x 5 x m x n = 50 mn
Area of 3rd rectangle = 20x2 x 5y2 = 20 x 5 x x2 x y2 = 100 x2y2
Area of 4th rectangle = 4x x 3x2 = 4 x 3 x x x x2 = 12x3
Area of 5th rectangle = 3mn x 4np = 3 x 4 x m x n x n x p = 12mn2p
Q3 : Complete the table of products.
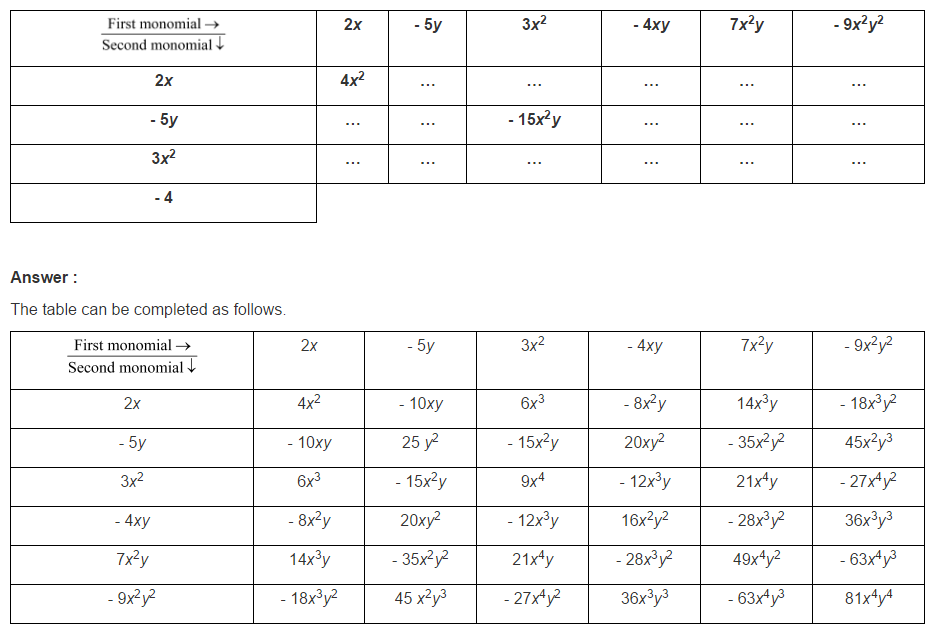
Q4 : Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a2, 7a4 (ii) 2p, 4q, 8r (iii) xy, 2x2y, 2xy2
(iv) a, 2b, 3c
Answer :
We know that,
Volume = Length x Breadth x Height
(i) Volume = 5a x 3a2 x 7a4 = 5 x 3 x 7 x a x a2 x a4 = 105 a7
(ii) Volume = 2p x 4q x 8r = 2 x 4 x 8 x p x q x r = 64pqr
(iii) Volume = xy x 2x2y x 2xy2 = 2 x 2 x xy x x2y x xy2 = 4x4y4
(iv) Volume = a x 2b x 3c = 2 x 3 x a x b x c = 6abc
Q5 : Obtain the product of
(i) xy, yz, zx (ii) a, – a2, a3 (iii) 2, 4y, 8y2, 16y3
(iv) a, 2b, 3c, 6abc (v) m, – mn, mnp
Answer :
(i) xy x yz x zx = x2y2z2
(ii) a x (- a2) x a3 = – a6
(iii) 2 x 4y x 8y2 x 16y3 = 2 x 4 x 8 x 16 x y x y2 x y3 = 1024 y6
(iv) a x 2b x 3c x 6abc = 2 x 3 x 6 x a x b x c x abc = 36a2b2c2
(v) m x (- mn) x mnp = – m3n2p
Exercise 9.3 : Solutions of Questions on Page Number : 146
Q1 : Carry out the multiplication of the expressions in each of the following pairs.
(i) 4p, q + r (ii) ab, a – b (iii) a + b, 7a2b2
(iv) a2 – 9, 4a (v) pq + qr + rp, 0
Answer :
(i) (4p) x (q + r) = (4p x q) + (4p x r) = 4pq + 4pr
(ii) (ab) x (a – b) = (ab x a) + [ab x (- b)] = a2b – ab2
(iii) (a + b) x (7a2 b2) = (a x 7a2b2) + (b x 7a2b2) = 7a3b2 + 7a2b3
(iv) (a2 – 9) x (4a) = (a2 x 4a) + (- 9) x (4a) = 4a3 – 36a
(v) (pq + qr + rp) x 0 = (pq x 0) + (qr x 0) + (rp x 0) = 0
Q2 : Complete the table
| — | First expression | Second Expression | Product |
| (i) | a | b + c + d | – |
| (ii) | x + y – 5 | 5 xy | – |
| (iii) | p | 6p2 – 7p + 5 | – |
| (iv) | 4p2q2 | p2 – q2 | – |
| (v) | a + b + c | abc | – |
Answer :
The table can be completed as follows.
| – | First expression | Second Expression | Product |
| (i) | a | b + c + d | ab + ac + ad |
| (ii) | x + y – 5 | 5 xy | 5x2y + 5xy2 – 25xy |
| (iii) | p | 6p2 – 7p + 5 | 6p3 – 7p2 + 5p |
| (iv) | 4p2q2 | p2 – q2 | 4p4q2 – 4p2q4 |
| (v) | a + b + c | abc | a2bc + ab2c + abc2 |
Q3 : Find the product.
(i) (a2) × (2a22) × (4a26)
(ii)![]() (iii)
(iii)![]()
(iv) x × x2 × x3 × x4
Answer :
(i) (a2) × (2a22) × (4a26) = 2 × 4 ×a2 × a22 × a26 = 8a50
(ii)![]()
(iii)![]()
(iv) x × x2 × x3 × x4 = x10
Q4 : (a) Simplify 3x (4x – 5) + 3 and find its values for (i) x = 3, (ii) ![]() .
.
(b) a (a2 + a + 1) + 5 and find its values for (i) a = 0, (ii) a = 1, (iii) a = – 1.
Answer :
(a) 3x (4x – 5) + 3 = 12x2 – 15x + 3
(i) For x = 3, 12x2 – 15x + 3 = 12 (3)2 – 15(3) + 3
= 108 – 45 + 3
= 66
(ii) For![]()
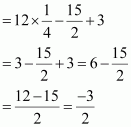
(b)a (a2 + a + 1) + 5 = a3 + a2 + a + 5
(i) For a = 0, a3 + a2 + a + 5 = 0 + 0 + 0 + 5 = 5
(ii) For a = 1, a3 + a2 + a + 5 = (1)3 + (1)2 + 1 + 5
= 1 + 1 + 1 + 5 = 8
(iii) For a = – 1, a3 + a2 + a + 5 = ( – 1)3 + ( – 1)2 + ( – 1) + 5
= – 1 + 1 – 1 + 5 = 4
Q5 : (a) Add: p (p – q), q (q – r) and r (r - p)
(b) Add: 2x (z – x – y) and 2y (z – y – x)
(c) Subtract: 3l (l – 4m + 5n) from 4l (10n – 3m + 2l)
(d) Subtract: 3a (a + b + c) – 2b (a – b + c) from 4c (- a + b + c)
Answer :
(a) First expression = p (p – q) = p2 – pq
Second expression = q (q – r) = q2 – qr
Third expression = r (r – p) = r2 – pr
Adding the three expressions, we obtain
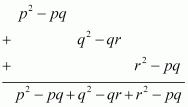
Therefore, the sum of the given expressions is p2 + q2 + r2 – pq – qr – rp.
(b) First expression = 2x (z – x – y) = 2xz – 2x2 – 2xy
Second expression = 2y (z – y – x) = 2yz – 2y2 – 2yx
Adding the two expressions, we obtain
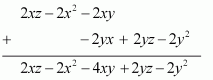
Therefore, the sum of the given expressions is – 2x2 – 2y2 – 4xy + 2yz + 2zx.
(c) 3l (l – 4m + 5n) = 3l2 – 12lm + 15ln
4l (10n – 3m + 2l) = 40ln – 12lm + 8l2
Subtracting these expressions, we obtain
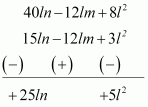
Therefore, the result is 5l2 + 25ln.
(d) 3a (a + b + c) – 2b (a – b + c) = 3a2 +3ab + 3ac – 2ba + 2b2 – 2bc
= 3a2 + 2b2 + ab + 3ac – 2bc
4c ( – a + b + c) = – 4ac + 4bc + 4c2
Subtracting these expressions, we obtain
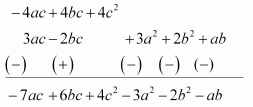
Therefore, the result is – 3a2 – 2b2 + 4c2 – ab + 6bc – 7ac.
Exercise 9.4 : Solutions of Questions on Page Number : 148
Q1 : Multiply the binomials.
(i) (2x + 5) and (4x – 3) (ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5m) and (2.5l + 0.5m) (iv) (a + 3b) and (x + 5)
(v) (2pq + 3q2) and (3pq – 2q2)
(vi)![]()
Answer :
(i) (2x + 5) × (4x – 3) = 2x × (4x – 3) + 5 × (4x – 3)
= 8x2 – 6x + 20x – 15
= 8x2 + 14x – 15 (By adding like terms)
(ii) (y – 8) × (3y – 4) = y × (3y – 4) – 8 × (3y – 4)
= 3y2 – 4y – 24y + 32
= 3y2 – 28y + 32 (By adding like terms)
(iii) (2.5l – 0.5m) × (2.5l + 0.5m) = 2.5l × (2.5l + 0.5m) – 0.5m (2.5l + 0.5m)
= 6.25l2 + 1.25lm – 1.25lm – 0.25m2
= 6.25l2 – 0.25m2
(iv) (a + 3b) × (x + 5) = a × (x + 5) + 3b × (x + 5)
= ax + 5a + 3bx + 15b
(v) (2pq + 3q2) × (3pq – 2q2) = 2pq × (3pq – 2q2) + 3q2 × (3pq – 2q2)
= 6p2q2 – 4pq3 + 9pq3 – 6q4
= 6p2q2 + 5pq3 – 6q4
(vi)![]()
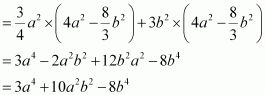
Q2 : Find the product.
(i) (5 – 2x) (3 + x) (ii) (x + 7y) (7x – y)
(iii) (a2 + b) (a + b2) (iv) (p2 – q2) (2p + q)
Answer :
(i) (5 – 2x) (3 + x) = 5 (3 + x) – 2x (3 + x)
= 15 + 5x – 6x – 2x2
= 15 – x – 2x2
(ii) (x + 7y) (7x – y) = x (7x – y) + 7y (7x – y)
= 7x2 – xy + 49xy – 7y2
= 7x2 + 48xy – 7y2
(iii) (a2 + b) (a + b2) = a2 (a + b2) + b (a + b2)
= a3 + a2b2 + ab + b3
(iv) (p2 – q2) (2p + q) = p2 (2p + q) – q2 (2p + q)
= 2p3 + p2q – 2pq2 – q3
Q3 : Simplify.
(i) (x2 – 5) (x + 5) + 25
(ii) (a2 + 5) (b3 + 3) + 5
(iii) (t + s2) (t2 – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
(v) (x + y) (2x + y) + (x + 2y) (x – y)
(vi) (x + y) (x2 – xy + y2)
(vii) (1.5x – 4y) (1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c) (a + b – c)
Answer :
(i) (x2 – 5) (x + 5) + 25
= x2 (x + 5) – 5 (x + 5) + 25
= x3 + 5x2 – 5x – 25 + 25
= x3 + 5x2 – 5x
(ii) (a2 + 5) (b3 + 3) + 5
= a2 (b3 + 3) + 5 (b3 + 3) + 5
= a2b3 + 3a2 + 5b3 + 15 + 5
=a2b3 + 3a2 + 5b3 + 20
(iii) (t + s2) (t2 – s)
= t (t2 – s) + s2 (t2 – s)
= t3 – st + s2t2 – s3
(iv) (a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
= a (c – d) + b (c – d) + a (c + d) – b (c + d) + 2 (ac + bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= (ac + ac + 2ac) + (ad – ad) + (bc – bc) + (2bd – bd – bd)
= 4ac
(v) (x + y) (2x + y) + (x + 2y) (x – y)
= x (2x + y) + y (2x + y) + x (x – y) + 2y (x – y)
= 2x2 + xy + 2xy + y2 + x2 – xy + 2xy – 2y2
= (2x2 + x2) + (y2 – 2y2) + (xy + 2xy – xy + 2xy)
= 3x2 – y2 + 4xy
(vi) (x + y) (x2 – xy + y2)
= x (x2 – xy + y2) + y (x2 – xy + y2)
= x3 – x2y + xy2 + x2y – xy2 + y3
= x3 + y3 + (xy2 – xy2) + (x2y – x2y)
= x3 + y3
(vii) (1.5x – 4y) (1.5x + 4y + 3) – 4.5x + 12y
= 1.5x (1.5x + 4y + 3) – 4y (1.5x + 4y + 3) – 4.5x + 12y
= 2.25 x2 + 6xy + 4.5x – 6xy – 16y2 – 12y – 4.5x + 12y
= 2.25 x2 + (6xy – 6xy) + (4.5x – 4.5x) – 16y2 + (12y – 12y)
= 2.25x2 – 16y2
(viii) (a + b + c) (a + b – c)
= a (a + b – c) + b (a + b – c) + c (a + b – c)
= a2 + ab – ac + ab + b2 – bc + ca + bc – c2
= a2 + b2 – c2 + (ab + ab) + (bc – bc) + (ca – ca)
= a2 + b2 – c2 + 2ab
Exercise 9.5 : Solutions of Questions on Page Number : 151
Q1 : Use a suitable identity to get each of the following products.
(i) (x + 3) (x + 3) (ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv)![]()
(v) (1.1m – 0.4) (1.1 m + 0.4) (vi) (a2 + b2) ( – a2 + b2)
(vii) (6x – 7) (6x + 7) (viii) ( – a + c) ( – a + c)
(ix)![]()
(x) (7a – 9b) (7a – 9b)
Answer :
The products will be as follows.
(i) (x + 3) (x + 3) = (x + 3)2
= (x)2 + 2(x) (3) + (3)2 [(a + b)2 = a2 + 2ab + b2]
= x2 + 6x + 9
(ii) (2y + 5) (2y + 5) = (2y + 5)2
= (2y)2 + 2(2y) (5) + (5)2 [(a + b)2 = a2 + 2ab + b2]
= 4y2 + 20y + 25
(iii) (2a – 7) (2a – 7) = (2a – 7)2
= (2a)2 – 2(2a) (7) + (7)2 [(a – b)2 = a2 – 2ab + b2]
= 4a2 – 28a + 49
(iv)![]()
![]() [(a – b)2 = a2 – 2ab + b2]
[(a – b)2 = a2 – 2ab + b2]
![]()
(v) (1.1m – 0.4) (1.1 m + 0.4)
= (1.1m)2 – (0.4)2 [(a + b) (a – b) = a2 – b2]
= 1.21m2 – 0.16
(vi) (a2 + b2) ( – a2 + b2) = (b2 + a2) (b2 – a2)
= (b2)2 – (a2)2 [(a + b) (a – b) = a2 – b2]
= b4 – a4
(vii) (6x – 7) (6x + 7) = (6x)2 – (7)2 [(a + b) (a – b) = a2 – b2]
= 36x2 – 49
(viii) ( – a + c) ( – a + c) = ( – a + c)2
= ( – a)2 + 2( – a) (c) + (c)2 [(a + b)2 = a2 + 2ab + b2]
= a2 – 2ac + c2
(ix)![]()
![]() [(a + b)2 = a2 + 2ab + b2]
[(a + b)2 = a2 + 2ab + b2]
![]()
(x) (7a – 9b) (7a – 9b) = (7a – 9b)2
= (7a)2 – 2(7a)(9b) + (9b)2 [(a – b)2 = a2 – 2ab + b2]
= 49a2 – 126ab + 81b2
Q2 : Use the identity (x + a) (x + b) = x2 + (a + b)x + ab to find the following products.
(i) (x + 3) (x + 7) (ii) (4x +5) (4x + 1)
(iii) (4x – 5) (4x – 1) (iv) (4x + 5) (4x – 1)
(v) (2x +5y) (2x + 3y) (vi) (2a2 +9) (2a2 + 5)
(vii) (xyz – 4) (xyz – 2)
Answer :
The products will be as follows.
(i) (x + 3) (x + 7) = x2 + (3 + 7) x + (3) (7)
= x2 + 10x + 21
(ii) (4x + 5) (4x + 1) = (4x)2 + (5 + 1) (4x) + (5) (1)
= 16x2 + 24x + 5
(iii)
![]()
= 16x2 – 24x + 5
(iv)![]()
= 16x2 + 16x – 5
(v) (2x +5y) (2x + 3y) = (2x)2 + (5y + 3y) (2x) + (5y) (3y)
= 4x2 + 16xy + 15y2
(vi) (2a2 +9) (2a2 + 5) = (2a2)2 + (9 + 5) (2a2) + (9) (5)
= 4a4 + 28a2 + 45
(vii) (xyz – 4) (xyz – 2)
=![]()
= x2y2z2 – 6xyz + 8
Q3 : Find the following squares by suing the identities.
(i) (b – 7)2 (ii) (xy + 3z)2 (iii) (6x2 – 5y)2
(iv)![]()
(v) (0.4p – 0.5q)2 (vi) (2xy + 5y)2
Answer :
(i) (b – 7)2 = (b)2 – 2(b) (7) + (7)2 [(a – b)2 = a2 – 2ab + b2]
= b2 – 14b + 49
(ii) (xy + 3z)2 = (xy)2 + 2(xy) (3z) + (3z)2 [(a + b)2 = a2 + 2ab + b2]
= x2y2 + 6xyz + 9z2
(iii) (6x2 – 5y)2 = (6x2)2 – 2(6x2) (5y) + (5y)2 [(a – b)2 = a2 – 2ab + b2]
= 36x4 – 60x2y + 25y2
(iv)![]()
![]() [(a + b)2 = a2 + 2ab + b2]
[(a + b)2 = a2 + 2ab + b2]
![]()
(v) (0.4p – 0.5q)2 = (0.4p)2 – 2 (0.4p) (0.5q) + (0.5q)2
[(a – b)2 = a2 – 2ab + b2]
= 0.16p2 – 0.4pq + 0.25q2
(vi) (2xy + 5y)2 = (2xy)2 + 2(2xy) (5y) + (5y)2
[(a + b)2 = a2 + 2ab + b2]
= 4x2y2 + 20xy2 + 25y2
Q4 : Simplify.
(i) (a2 – b2)2 (ii) (2x +5)2 – (2x – 5)2
(iii) (7m – 8n)2 + (7m + 8n)2 (iv) (4m + 5n)2 + (5m + 4n)2
(v) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
(vi) (ab + bc)2 – 2ab2c (vii) (m2 – n2m)2 + 2m3n2
Answer :
(i) (a2 – b2)2 = (a2)2 – 2(a2) (b2) + (b2)2 [(a – b)2 = a2 – 2ab + b2 ]
= a4 – 2a2b2 + b4
(ii) (2x +5)2 – (2x – 5)2 = (2x)2 + 2(2x) (5) + (5)2 – [(2x)2 – 2(2x) (5) + (5)2]
[(a – b)2 = a2 – 2ab + b2]
[(a + b)2 = a2 + 2ab + b2]
= 4x2 + 20x + 25 – [4x2 – 20x + 25]
= 4x2 + 20x + 25 – 4x2 + 20x – 25 = 40x
(iii) (7m – 8n)2 + (7m + 8n)2
= (7m)2 – 2(7m) (8n) + (8n)2 + (7m)2 + 2(7m) (8n) + (8n)2
[(a – b)2 = a2 – 2ab + b2 and (a + b)2 = a2 + 2ab + b2]
= 49m2 – 112mn + 64n2 + 49m2 + 112mn + 64n2
= 98m2 + 128n2
(iv) (4m + 5n)2 + (5m + 4n)2
= (4m)2 + 2(4m) (5n) + (5n)2 + (5m)2 + 2(5m) (4n) + (4n)2
[ (a + b)2 = a2 + 2ab + b2]
= 16m2 + 40mn + 25n2 + 25m2 + 40mn + 16n2
= 41m2 + 80mn + 41n2
(v) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
= (2.5p)2 – 2(2.5p) (1.5q) + (1.5q)2 – [(1.5p)2 – 2(1.5p)(2.5q) + (2.5q)2]
[(a – b)2 = a2 – 2ab + b2 ]
= 6.25p2 – 7.5pq + 2.25q2 – [2.25p2 – 7.5pq + 6.25q2]
= 6.25p2 – 7.5pq + 2.25q2 – 2.25p2 + 7.5pq – 6.25q2]
= 4p2 – 4q2
(vi) (ab + bc)2 – 2ab2c
= (ab)2 + 2(ab)(bc) + (bc)2 – 2ab2c [(a + b)2 = a2 + 2ab + b2 ]
= a2b2 + 2ab2c + b2c2 – 2ab2c
= a2b2 + b2c2
(vii) (m2 – n2m)2 + 2m3n2
= (m2)2 – 2(m2) (n2m) + (n2m)2 + 2m3n2 [(a – b)2 = a2 – 2ab + b2 ]
= m4 – 2m3n2 + n4m2 + 2m3n2
= m4 + n4m2
Q5 :Show that
(i) (3x + 7)2 – 84x = (3x – 7)2 (ii) (9p – 5q)2 + 180pq = (9p + 5q)2
(iii)![]()
(iv) (4pq + 3q)2 – (4pq – 3q)2 = 48pq2
(v) (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
Answer :
(i) L.H.S = (3x + 7)2 – 84x
= (3x)2 + 2(3x)(7) + (7)2 – 84x
= 9x2 + 42x + 49 – 84x
= 9x2 – 42x + 49
R.H.S = (3x – 7)2 = (3x)2 – 2(3x)(7) +(7)2
= 9x2 – 42x + 49
L.H.S = R.H.S
(ii) L.H.S = (9p – 5q)2 + 180pq
= (9p)2 – 2(9p)(5q) + (5q)2 – 180pq
= 81p2 – 90pq + 25q2 + 180pq
= 81p2 + 90pq + 25q2
R.H.S = (9p + 5q)2
= (9p)2 + 2(9p)(5q) + (5q)2
= 81p2 + 90pq + 25q2
L.H.S = R.H.S
(iii) L.H.S =
![]()
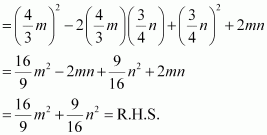
(iv) L.H.S = (4pq + 3q)2 – (4pq – 3q)2
= (4pq)2 + 2(4pq)(3q) + (3q)2 – [(4pq)2 – 2(4pq) (3q) + (3q)2]
= 16p2q2 + 24pq2 + 9q2 – [16p2q2 – 24pq2 + 9q2]
= 16p2q2 + 24pq2 + 9q2 – 16p2q2 + 24pq2 – 9q2
= 48pq2 = R.H.S
(v) L.H.S = (a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a)
= (a2 – b2) + (b2 – c2) + (c2 – a2) = 0 = R.H.S.
Q6 : Using identities, evaluate.
(i) 712 (ii) 992 (iii) 1022 (iv) 9982
(v) (5.2)2 (vi) 297 x 303 (vii) 78 x 82
(viii) 8.92 (ix) 1.05 x 9.5
Answer :
(i) 712 = (70 + 1)2
= (70)2 + 2(70) (1) + (1)2 [(a + b)2 = a2 + 2ab + b2 ]
= 4900 + 140 + 1 = 5041
(ii) 992 = (100 – 1)2
= (100)2 – 2(100) (1) + (1)2 [(a – b)2 = a2 – 2ab + b2 ]
= 10000 – 200 + 1 = 9801
(iii) 1022 = (100 + 2)2
= (100)2 + 2(100)(2) + (2)2 [(a + b)2 = a2 + 2ab + b2 ]
= 10000 + 400 + 4 = 10404
(iv) 9982 = (1000 – 2)2
= (1000)2 – 2(1000)(2) + (2)2 [(a – b)2 = a2 – 2ab + b2 ]
= 1000000 – 4000 + 4 = 996004
(v) (5.2)2 = (5.0 + 0.2)2
= (5.0)2 + 2(5.0) (0.2) + (0.2)2 [(a + b)2 = a2 + 2ab + b2 ]
= 25 + 2 + 0.04 = 27.04
(vi) 297 x 303 = (300 – 3) x (300 + 3)
= (300)2 – (3)2 [(a + b) (a – b) = a2 – b2]
= 90000 – 9 = 89991
(vii) 78 x 82 = (80 – 2) (80 + 2)
= (80)2 – (2)2 [(a + b) (a – b) = a2 – b2]
= 6400 – 4 = 6396
(viii) 8.92 = (9.0 – 0.1)2
= (9.0)2 – 2(9.0) (0.1) + (0.1)2 [(a – b)2 = a2 – 2ab + b2 ]
= 81 – 1.8 + 0.01 = 79.21
(ix) 1.05 x 9.5 = 1.05 x 0.95 x 10
= (1 + 0.05) (1- 0.05) x 10
= [(1)2 – (0.05)2] x 10
= [1 – 0.0025] x 10 [(a + b) (a – b) = a2 – b2]
= 0.9975 x 10 = 9.975
Q7 : Using a2 – b2 = (a + b) (a – b), find
(i) 512 – 492 (ii) (1.02)2 – (0.98)2 (iii) 1532 – 1472
(iv) 12.12 – 7.92
Answer :
(i) 512 – 492 = (51 + 49) (51 – 49)`
= (100) (2) = 200
(ii) (1.02)2 – (0.98)2 = (1.02 + 0.98) (1.02 - 0.98)
= (2) (0.04) = 0.08
(iii) 1532 – 1472 = (153 + 147) (153 – 147)
= (300) (6) = 1800
(iv) 12.12 – 7.92 = (12.1 + 7.9) (12.1 – 7.9)
= (20.0) (4.2) = 84
Q8 : Using (x + a) (x + b) = x2 + (a + b) x + ab, find
(i) 103 x 104 (ii) 5.1 x 5.2 (iii) 103 x 98 (iv) 9.7 x 9.8
Answer :
(i) 103 x 104 = (100 + 3) (100 + 4)
= (100)2 + (3 + 4) (100) + (3) (4)
= 10000 + 700 + 12 = 10712
(ii) 5.1 x 5.2 = (5 + 0.1) (5 + 0.2)
= (5)2 + (0.1 + 0.2) (5) + (0.1) (0.2)
= 25 + 1.5 + 0.02 = 26.52
(iii) 103 x 98 = (100 + 3) (100 – 2)
= (100)2 + [3 + (- 2)] (100) + (3) (- 2)
= 10000 + 100 – 6
= 10094
(iv) 9.7 x 9.8 = (10 – 0.3) (10 – 0.2)
= (10)2 + [(- 0.3) + (- 0.2)] (10) + (- 0.3) (- 0.2)
= 100 + (- 0.5)10 + 0.06 = 100.06 – 5 = 95.06